Display table¶
Goal¶
Display an Orange Textable table.
Prerequisites¶
Some text has been imported in Orange Textable (see Cookbook: Text input) and possibly further processed (see Cookbook: Segmentation manipulation). A table has been created by means of one of Orange Textable’s table construction widgets (see Cookbook: Text analysis).
Procedure¶
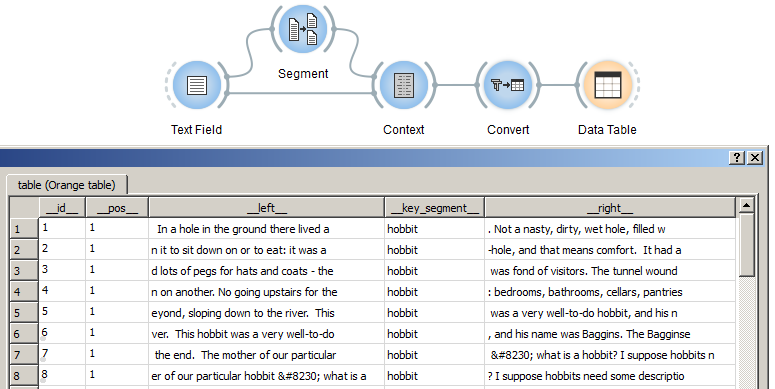
Figure 1: Display an Orange Textable table with instances of Convert and Data Table.
- Create an instance of Convert and Data Table on the canvas (the latter is found in the Data tab of Orange Canvas).
- Drag and drop from the output connection (righthand side) of the widget instance that has been used to build a table (e.g. Context) to the Convert widget instance’s input connection (lefthand side).
- Connect the Convert instance to the Data Table instance.
- Open the Data Table instance’s interface by double-clicking on its icon on the canvas to display the table.
Comment¶
- If the table is a frequency table, you may want to change its default orientation of the table to make it easier to read. To that effect, open the Convert instance’s interface, tick the Advanced settings checkbox, and in the Transform section, tick the transpose checkbox.
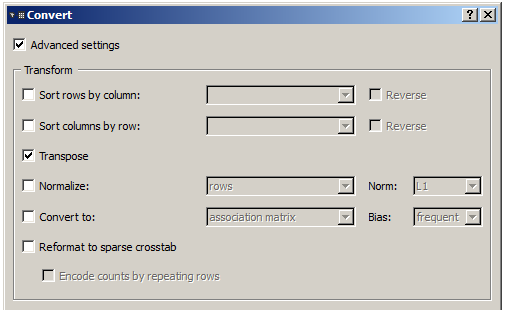
Figure 2: Change the orientation of an Orange Textable frequency table using an instance of Convert.

