2.3. Counting segment types¶
Widget Count takes in input one or more segmentations and
produces frequency tables such as tables 1 and 2
here. To try it out, create a schema such as
illustrated on figure 1 below. As usual,
we will suppose that the Text Field instance contains
a simple example. The Segment instance is configured for
letter segmentation (Regex: \w and Output segmentation label:
letters). The default configuration of the instances of
Convert and Data Table (from the Data tab of Orange
Canvas) needs not be modified for this example.

Figure 1: Schema for testing the Count widget.
Basically, the purpose of widget Count is to determine the frequency of segment types in an input segmentation. The label of that segmentation must be indicated in the Segmentation menu of section Units in the widget’s interface, while other controls may be left in their default state for now (see figure 2 below). Clicking Compute then double-clicking the Data Table instance should display essentially the same data as table 1 here (with possible variations in the order of columns).
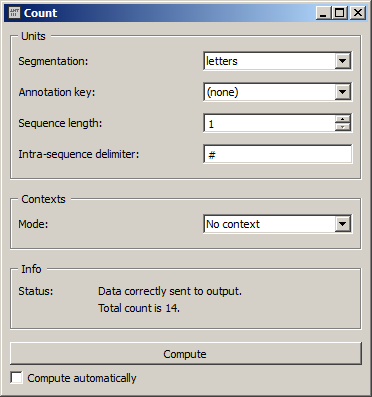
Figure 2: Counting the frequency of letter types with widget Count.
Note that checkbox Compute automatically is unchecked by default so that the user must click on Compute to trigger computations. The motivation for this default setting is that table construction widgets can be quite slow when operating on large segmentations, and it can be annoying to see computations starting again whenever an interface element is modified.
To obtain the frequency of letter bigrams (i.e. pairs of successive letters), simply set parameter Sequence length to 2 (see table 1 below). If the value of this parameter is greated than 1, the string specified in field Intra-sequence delimiter is inserted between successive segments for the sake of readability–which is more useful when segments are longer than individual letters. Note that in this example, word boundaries are not taken into account–nor even known, in fact–which is why bigrams as and ee have a nonzero frequency.
| as | si | im | mp | pl | le | ee | ex | xa | am |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 2 | 2 | 2 | 1 | 1 | 1 | 1 |