Count occurrences of smaller units in larger segments¶
Goal¶
Count the occurrences of smaller units (for instance letters) in larger segments (for instance words), and report the results by means of a two-dimensional contingency table (e.g. with words in rows and letters in columns).
Prerequisites¶
Some text has been imported in Orange Textable (see Cookbook: Text input) and it has been segmented in at least two hierarchical levels, e.g. words and letters (see Cookbook: Segment text in smaller units).
Procedure¶
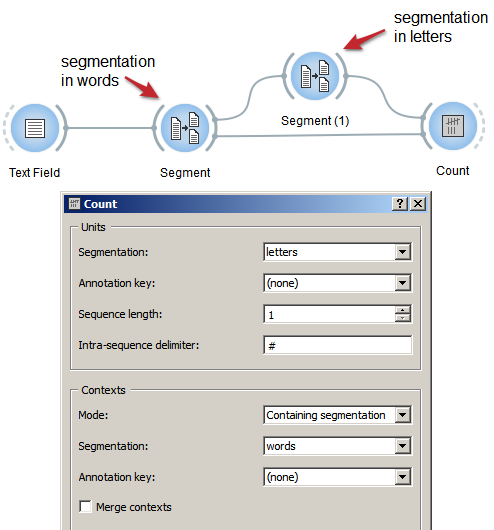
Figure 1: Count occurrences of smaller units in larger segments with an instance of Count
- Create an instance of Count on the canvas.
- Drag and drop from the output connection (righthand side) of both widget instances that have been used to segment the text (here the two instances of Segment) to the Count widget instance’s input connection (lefthand side), thus forming a triangle.
- Open the Count instance’s interface by double-clicking on its icon on the canvas.
- In the Units section, select the segmentation into smaller units (here: letters).
- In the Context section, choose Mode: Containing segmentation.
- In the Segmentation field, select the context segmentation, i.e. the segmentation into larger segments (here words).
- Click the Compute button (or make sure the Compute automatically checkbox is selected).
- A table showing the results is then available at the output connection of the Count instance; to display or export it, see Cookbook: Table output.
Comment¶
- The total number of segments in your segmentation appears in the Info section (here: 14).
- It is also possible to define units as segment pairs (bigrams), triples (trigrams), and so on, by increasing the Sequence length parameter in the Units section.
- If Sequence length is set to a value greater than 1, the string
appearing in the Intra-sequence delimiter field will be inserted between
the elements composing each n-gram in the column headers, which can
enhance their readability. The default is
#but you can change it by inserting the delimiter of your choice.
